링크
문제 요약
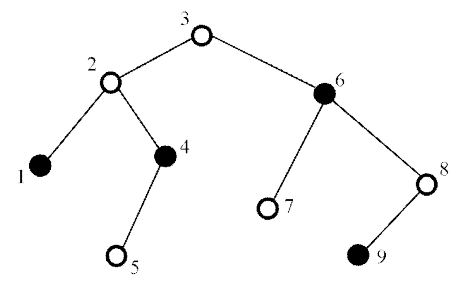
정점의 개수가 $N$개인 트리가 주어지고 각 정점에는 검은 돌이 1개 놓여있거나 없는 상태며, 전체 트리에는 총 $B$개의 검은 돌이 놓여져 있다. 주어진 트리에서 정점의 개수가 정확히 $i$개이며 검은 돌의 개수가 $j$개인 서브트리가 존재하는지에 대한 쿼리가 들어온다. 이때 주어진 쿼리들 중 답이 “존재한다” 인 쿼리의 개수를 구하여라.
관찰
주어진 문제가 모든 서브트리에 대하여 조사를 해야 답이 나오기 때문에 트리 DP를 고려해볼 수 있다. 즉, 기본적인 아이디어는 들어올 수 있는 모든 쿼리 ($O(N^2)$가지) 에 대한 존재 여부를 모두 전처리로 계산해 놓고, 입력으로 들어온 쿼리에 대한 답을 상수 시간에 찾는 것이다. 따라서 주어진 트리를 1번 정점을 루트로 할 때, 아래와 같은 형태의 점화식을 생각해 볼 수 있다.
$D(i,j,k)=i$번 노드가 루트인 서브트리 중, 크기가 $j$이고 $k$개의 검은 돌을 갖는 서브트리의 존재성
$D(i,1,0)=$ true ($i$번 노드가 흰색) 또는 $D(i,1,1)=$ true ($i$번 노드가 검은색) $\hspace{2em}$ (Base Case)
$D(i,j,k)=D(i,j_1,k_1)\&D(i’,j_2,k_2) \hspace{1em}(\mathrm{where} \hspace{0.5em} j_1+j_2=j, k_1+k_2=k, i’\in{}\mathrm{childs \hspace{0.5em} of}\hspace{0.5em}i)$
이때 실제로 값을 계산하여 저장할 때는 중복을 막기 위해 $j$ 와 $k$는 큰 값부터 계산한다.
이렇게 Naive한 DP를 사용할 경우 자명하게 상태의 개수가 $O(N^2B)$개, 상태의 전이에 $O(NB)$ 의 시간이 걸리므로, $O(N^3B^2)=O(N^5)$ 이 된다.
위와 같은 기본적인 점화식을 구하게 되면, 이제 점화식의 구조나, DP 테이블에 값이 채워지는 형태 등의 특성을 바탕으로 최적화 작업을 해야 한다. 점화식의 구조가 최적화가 되는 특정한 형태로는 안 보이니, 문제에 주어진 예시로 위의 DP 테이블을 각각 적어보도록 하자.
 |
|---|
| Figure 1 |
예시 이미지의 루트가 3인 관계로 루트를 3으로 하는 트리에 대하여 위의 점화식을 수행한 결과물이다. 값이 1은 해당 경우가 존재함을 의미하며 아무것도 적히지 않은 경우 존재하지 않음을 의미한다.
$D(5,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(9,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(1,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(4,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | 1 | ||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(7,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(8,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | 1 | ||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(2,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | 1 | ||||
| 3 | 1 | 1 | |||
| 4 | 1 | ||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(6,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | 1 | ||||
| 3 | 1 | 1 | |||
| 4 | 1 | ||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
$D(3,i,j)$
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | 1 | ||||
| 2 | 1 | 1 | |||
| 3 | 1 | ||||
| 4 | 1 | 1 | |||
| 5 | 1 | 1 | 1 | ||
| 6 | 1 | 1 | |||
| 7 | 1 | 1 | 1 | ||
| 8 | 1 | 1 | |||
| 9 | 1 |
위의 DP 테이블을 살펴보면 알 수 있듯이 각 열에 대하여, 값이 1인 시작점과 끝점 사이의 모든 값이 연속적이란 것을 관찰 할 수 있다. 이는 단순히 우연이 아니며, 크기가 $j$인 각 서브트리에 대하여 검은 돌이 $k$개인 가장 작은 서브트리부터 가장 큰 서브트리까지 확장하는 과정을 생각해보면 자명한 결과임을 알 수 있다. 따라서 아래와 같은 Lemma를 얻을 수 있다.
Lemma) DP 테이블의 각 열에 대하여 true 값은 반드시 연속적으로 나타난다.
풀이
따라서 위의 Lemma로부터 DP 테이블의 인자를 줄일 수 있을 것이다. 새롭게 DP 테이블을 정의하고 점화식을 유도해보자.
$D(i,j,0)=i$번 노드를 루트로 하는 서브트리 중 $j$개의 검은 돌을 포함하는 가장 작은 서브트리의 크기
$D(i,j,1)=i$번 노드를 루트로 하는 서브트리 중 $j$개의 검은 돌을 포함하는 가장 큰 서브트리의 크기
$D(i,j,0)=\min{(D(i,j_1,0)+D(i’,j_2,0))} \hspace{1em} (\mathrm{where} \hspace{0.5em} j_1+j_2=j)$
$D(i,j,1)=\max{(D(i,j_1,1)+D(i’,j_2,1))} \hspace{1em} (\mathrm{where} \hspace{0.5em} j_1+j_2=j)$ 이때 $i’$ 은 $i$의 자식노드이며, 현 상태에 위의 식으로 값을 누적하는 형태로 업데이트 된다.
이렇게 점화식을 바꾸게 되면, 상태 공간의 개수는 $O(NB)$개 이고, 전이에 $O(B)$번이 필요하므로, $O(NB^2)=O(N^3)$가 된다.
여기까지 풀이가 나왔다면 더 이상 점화식을 최적화 할 수 있는 부분은 존재하지 않는다. 하지만 위의 풀이는 더 이상 개선할 필요가 없으며, 위의 점화식을 계산하는 자명한 코드를 작성하면 총 연산 횟수는 다음과 같다.
$\displaystyle{} \sum{}\min{(sz(L),B)}\times{}\min{(sz(R),B)}=O(NB)$
(이때 $L$과 $R$은 각 단계에 합쳐지는 두 트리를 의미하며, sz는 그 트리의 크기를 의미한다.) 즉, $O(N^3)$ 인줄 알았던 코드가 정확히 시간을 계산하면 $O(N^2)$이 된다는 것이다. 이에 대한 증명은 아래 링크를 참조하도록 하자.
증명 링크
위의 사실에 따라 시간 복잡도 $O(NB)=O(N^2)$에 DP 테이블을 채울 수 있고, 이를 바탕으로 쿼리가 들어올 수 있는 모든 경우에 대하여 $O(N^2)$에 대하여 그러한 서브 트리의 존재 여부를 알아낼 수 있다. 따라서 전체 시간 복잡도 $O(N^2)$에 문제가 해결되게 된다.