링크
BOJ 5471 Pyramid Base
BOJ 11552 Pyramid Base 2
문제 요약
M by N 크기의 격자상에 직사각형 모양 장애물이 놓여있다. 각 장애물을 제거하는데 드는 비용이 주어질 때, 예산 B 이하의 비용으로 장애물을 적절히 제거하여 장애물이 없는 최대 크기 정사각형을 구하여라. 단, 첫번째 문제에서 B=0이고 장애물을 최대 1000개 이다. 두번째 문제는 B가 최대 20억이고 장애물은 최대 30000개 이다.
관찰
가장 기본적으로 할 수 있는 생각은 만약 정답이 $W$ 라면, 자명히 $W’\leq{W}$ 에 대하여 한 변의 길이가 $W’$ 인 정사각형 역시 존재한다는 점이다. 즉, 존재성이 이분적이므로 Parametric Search를 이용하여 문제를 해결해 볼 수 있을 것이다. 적절한 결정 함수를 만들 수 있다면 문제는 이제 쉽게 해결된다.
풀이
결정 함수를 만드는 건 상당히 자명하다. 스위핑을 하며 최솟값 세그먼트 트리에 장애물을 추가하는 방식으로 문제를 해결하자. 즉, 아래와 같이 각각의 정사각형과 겹치는 장애물의 비용을 각 노드에 저장하는 것이다. 아래 그림의 경우 한 변의 길이가 3인 경우를 나타내었고 첫 3개의 노드만 영역을 표시하였다.
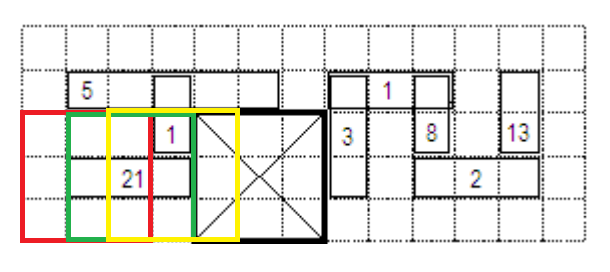 |
|---|
| Figure 1 |
원하는 정사각형이 존재하는지 여부는 세그먼트 트리의 최솟값이 B이하인지를 확인하면 된다. 이런식으로 하면 각 장애물은 1번 추가되고 1번 제거되므로, $O(P\log{N})$ 만큼의 시간을 최솟값 세그먼트 트리를 업데이트 하는데 사용된다. 따라서 Parametric Search를 하는데 드는 시간을 포함하면 $O(P\log{\min(M,N)}\log{N})$ 의 시간에 문제를 해결할 수 있다.
P.S. 추가적으로 구현상에 신경쓸 부분은 항상 최솟값은 1번 노드에 있으므로 상수시간에 최솟값을 확인해야 TLE를 면할 수 있다.