링크
문제 요약
여러개의 블럭이 쌓아서 만든 요새에 대하여, 각 위치별로 폭격을 가할 때 파괴되는 블럭의 개수를 찾는 문제이다.
관찰
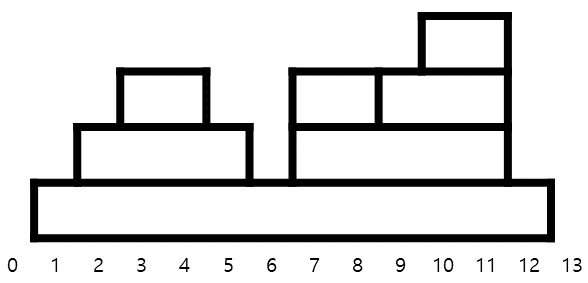
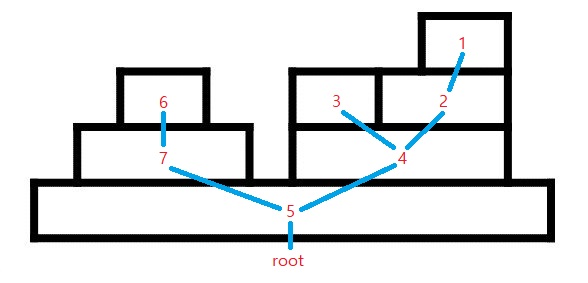
문제의 주어진 조건을 잘 살펴보면 주어진 요새는 반드시 트리의 형태를 띄게 됨을 알 수 있다. 아무런 블럭이 없는 땅을 root 라고 하면, 각 블럭에 대하여 자신의 바로 위에 직접적으로 쌓인 블럭이 자신의 자식 노드가 된다. 문제에 주어진 예제는 다음과 같이 거꾸로 뒤집어진 트리라고 볼 수 있다. 블럭의 번호는 예제 입력으로 주어진 번호를 사용하였다.
 |
 |
|---|---|
| Figure 1 | Figure 2 |
문제에서 어느 블럭이 폭격을 맞아서 사라진다는 것은 자신의 부모 노드와 자신이 하나의 노드로 합쳐진다는 것을 의미하고, 이는 문제에 주어진 예제 그림을 트리로 표현하면 이해할 수 있을 것이다. 그렇다면 이 과정을 효율적으로 하는 것이 곧 이 문제를 해결할 수 있게 할 것이다.
풀이
블럭이 사라진다는 것을 자식노드와 부모노드가 서로 합쳐진다는 관점으로 해석하게 되면, 이는 Disjoint set(=DSU)으로 둘을 union 하는 연산을 통해 쉽게 해결할 수 있게 된다. 이렇게 구현을 하면 좋은점이 상당히 많은데, 굳이 트리를 재구축하지 않고, 한번 만들어 놓은 트리를 그대로 사용할 수 있기 때문이다.
이게 무슨 뜻이냐면 폭격의 시작 노드를 쉽게 찾을 수 있다는 뜻이다. Sweeping 이나 이분 탐색등을 이용해서 최초의 요새 상태에서 폭격을 맞는 가장 윗 블럭을 찾았다고 하자. 그렇다면 DSU 에서 find 연산을 한 결과물은 현재까지의 폭격을 반영했을 때, 이번 폭격의 시작 위치임을 알 수 있다. 따라서 폭격을 가하는 행위는 find 연산과 union 연산을 번갈아 가며 반복수행하면 해결이 됨을 알 수 있다.
풀이를 종합하면 아래와 같다.
- Sweeping 으로 최초의 요새 상태를 트리로 바꾼다. 즉, 각 노드별로 parent를 찾는다.
- Sweeping 또는 이분 탐색을 이용해서 최초의 요새에서 각 폭격 위치별 최상단 블럭을 찾는다.
- DSU 로 find 와 union 연산을 반복하여 문제를 해결한다.
Sweeping 을 위해서는 정렬이 필요하므로, $O(N\log{N})$ 의 시간이 걸리게 된다. 또한 3번 과정의 경우 블록이 파괴되는 횟수는 N번을 넘을 수 없고, 한번의 연산을 할 때 union 과 find 가 1번씩 사용되므로 총 $O(N\alpha{(N)})$ 의 시간이 걸린다. 따라서 전체 시간 복잡도는 $O(N(\log{N}+\alpha{(N)}))$ 이 된다.
P.S. 사실 이 문제는 1년 전에 군복무 중에 만든 문제이다. 하지만 그 이외 작업을 할 여건이 안되서 문제 제작을 제외한 테스트 케이스 제작 및 검수 등의 모든 작업을 sonho00님이 도맡아 하여 출제가 되었다. 또한 최초의 풀이는 오프라인 쿼리와 세그먼트 트리를 이용한 복잡한 풀이였으나, hojoon0205님의 위와 같은 기막힌 풀이법으로 해당 방법이 정해로 채택되었다.