링크

문제 요약

좌표 평면 상에 $N$ 개의 점이 있을 때, $x$ 축에 평행한 직선 $l_1$ 과 $y$ 축에 평행한 직선 $l_2$ 를 생각하자. 이때 $i$번째 점으로부터 직선 $l_1$ 과 $l_2$ 중 가까운 거리를 $d_i$ 라고 하면, 각 직선을 적절히 위치시켜 $\max d_i$ 의 최솟값을 구하는 문제이다.

관찰

문제에서 요구하는 바가, 최댓값의 최소화이므로 Parametric Search 를 이용해야 될 것이라는 추측이 가능하다. 자명히 Parametric Search 를 위해 사용할 파라미터는 각 점으로부터 직선까지의 최소 거리일 것이다. 또한 아래 그림과 같은 상황을 생각해 보자.


Figure 1	Figure 2

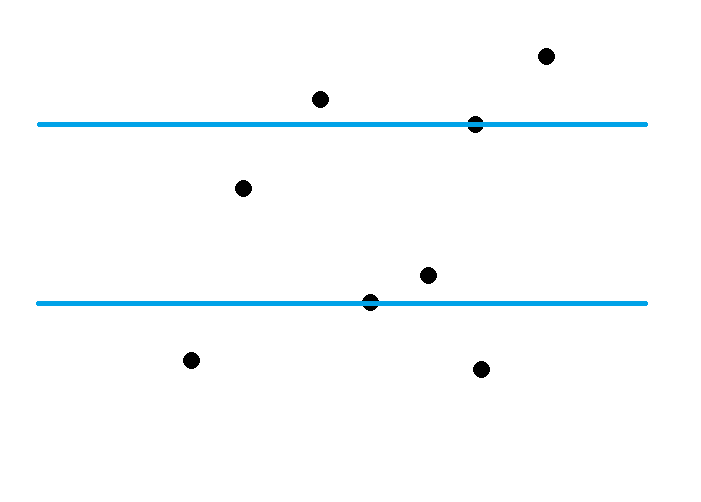
만약 Figure 1 과 같이 입력이 주어졌을 때, Figure 2 처럼 직선 $l_1$ 하늘색 구간의 점들을 커버한다면, 현재 커버되지 못한 점들은 모두 직선 $l_2$ 가 담당해야 한다. 즉, 직선 $l_1$ 의 위치를 점점 위로 올려보면서, 커버되지 못하는 점들을 직선 $l_2$ 가 담당할 때, 필요한 폭이 결정 함수로 주어진 폭으로 가능한지를 확인해 보면 될 것이다.

풀이

사실상 관찰에서 다룬 내용이 풀이의 전부이다. 단지 구현의 편의를 위해 직선으로부터 거리보다는 각 직선이 커버할 구간의 길이를 파라미터로 하는 것이 좋다. 우선 주어진 점들을 pair를 이용하여 정렬한다. 이후 결정 함수에서 앞서 관찰 내용을 구현하면 된다. 이를 위해서는 투 포인터를 이용하여 현재 직선 $l_1$ 이 커버 가능한 범위를 스위핑하며, 커버되지 못한 점들의 $x$ 좌표의 최솟값과 최댓값의 차이를 확인하면 된다.

따라서 커버되지 못한 점들의 $x$ 좌표의 최솟값과 최댓값의 차이를 효율적으로 알아야 한다. 이는 전처리를 2개 함으로써 알 수 있는데, 직선 $l_1$ 이 커버하는 구간이 배열에서 연속적이라는 점을 이용하면 된다. 현재 $[s,f]$ 를 커버한다고 하자, 그러면 $[1,s)$ 와 $(f,N]$ 에서의 x 값의 최대/최소를 알면 된다. 따라서 해당 내용을 전처리를 통해 $O(N)$ 에 구할 수 있고, 결정 함수의 시간 복잡도 역시 투 포인터를 이용한 스위핑만 고려하면 되므로 $O(N)$ 이 된다.

전체 시간 복잡도는 다음과 같다. 점들을 정렬하는데 $O(N\log{N})$ , Parametric Search가 $O(\log{ (2\times{10^9}) })$ , 결정 함수가 $O(N)$ 이므로, 총 $O(N\log{N}+N\log{ (2\times{10^9}) })$ 가 된다.