링크

문제 요약

$1, 2, \cdots{}, n$ 로 이루어진 임의의 교란 순열 $D$ 에 대하여, $f(D)$ 를 $D$ 를 $k(1\leq{k}\leq{n})$ 만큼 rotation을 시킨 결과물 중에 여전히 교란 순열인 개수라고 정의하자. 이때, $f(D)=n-2$ 인 경우의 수를 $p$로 나눈 나머지를 구하여라.

관찰

만약 어떤 교란 순열 $D$ 가 $f(D)=n-2$ 를 만족하면, 이를 rotation한 결과물 중 여전히 교란 순열인 케이스 역시 정답이 된다. 따라서 rotation을 했을 때 서로 같은 순열을 제외한 경우의 수 $S$ 를 세고, $S\times{(n-2)}\pmod{p}$ 를 하면 정답이 나올 것이다. 두번째 예제에 이 사실을 적용한 결과물은 아래와 같다. (즉, 회전시켜 같은 순열들을 제외한 결과물이다.)

4 3 6 5 2 1
5 6 4 2 3 1
6 3 2 5 4 1
5 3 4 2 6 1
6 4 5 3 1 2

또한 $f(D)=n-2$ 인 교란 순열 $D$ 의 의미를 생각해보자. 해당 케이스들의 경우 순열을 회전시킨 결과물이 각각 자신의 자리를 되찾는 순간이 단 2번 존재한다는 뜻이다. 또한 어떤 교란 순열이든 $k(1\leq{k}\leq{n})$ 만큼 회전을 시킨 결과물 중에 숫자 1이 첫번째 위치에 오는 경우의 수는 반드시 존재하고, 이 경우는 교란 순열이 아니다. 따라서 편의상 위의 순열들을 첫번째 숫자가 1이 되도록 새롭게 재배열하자.

1 4 3 6 5 2
1 5 6 4 2 3
1 6 3 2 5 4
1 5 3 4 2 6
1 2 6 4 5 3

이렇게 배열하면 $f(D)=n-2$ 인 교란 순열 $D$ 의 의미는 현재 상태에서 이미 $i=p_i$ 인 경우를 제외한 나머지 숫자들이 어떤 특정 칸 만큼 회전을 시키면, 해당 숫자들이 동시에 모두 자신의 자리를 되찾는 경우가 딱 1번 추가적으로 존재한다는 뜻이 된다.

풀이

이제 아래와 같이 그림을 그려보자. 아래 그림에서 파란색은 이미 $i=p_i$ 인 경우를 색칠한 것이다. 위의 예시에서 1번째와 3번째 케이스가 아래 그림 중 첫번째에 해당이 된다. 또한 2번째 케이스가 2번째 그림, 4번째 케이스가 3번째 그림, 5번째 케이스가 4번째 그림에 해당됨을 알 수 있을 것이다.

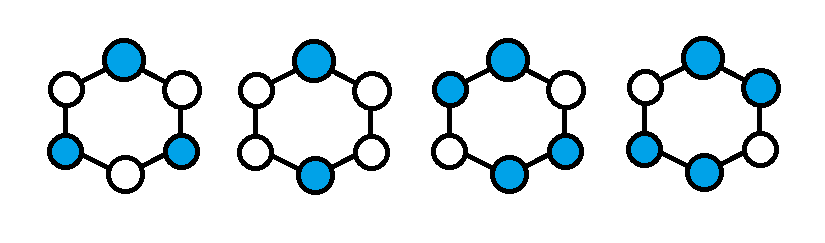
(가운데 맨위 점이 1번이다. 현재 풀이에서 1번이 자기자리에 배치되는 상황으로 경우를 분류하고 있으므로 4개의 그림 모두 해당 칸이 색칠되어있다.)

각 그림을 관찰하면, 첫번째 그림은 [1,2], [3,4], [5,6] 이 서로 패턴이 같고, 나머지 그림들은 [1,3],[4,6] 이 패턴이 같음을 알 수 있다. 이때, 3번째 그림과 4번째 그림이 서로 같은 상황 아니냐고 의문을 가질 수 있지만, 색칠의 의미는 자신의 위치에 자기자신 숫자가 들어온 경우를 의미하므로 서로 다르게 구분해야 된다. 따라서 패턴의 주기 역시 [1,k] 를 기준 (항상 첫 구간의 시작점이 1번)으로 잡아야 한다.

이렇게 구분을 하고나면 이제 빈칸에 숫자를 배치하는 경우의 수를 따져야 한다. 빈칸에 숫자를 배치하는 경우의 수는 자명히 (전체 구간의 개수)-1 이 된다. 예를 들어 첫번째 그림은, 빈칸에 (2, 4, 6) 을 순서대로 넣는 경우를 제외하고 (4, 6, 2) 또는 (6, 2, 4) 를 배치해야 조건을 만족함을 알 수 있다. 이제 색칠을 하는 경우의 수를 구해야 하는데, 만약 전체 칸을 $d$ 개로 쪼갰다고 할 때, $2^{(n/d)-1}-1$ 가지가 된다. 왜냐하면 각 구간에 대하여 총 $(n/d)-1$ 개의 칸들을 색칠을 할 것인지 아닌지 결정하는 문제이기 때문이다.

지금까지 내용을 종합하면 색칠하는 경우의 수가 $2^{(n/d)-1}-1$ 가지, 빈칸에 숫자를 적는 경우가 $d-1$ 가지 이므로 아래와 같은 결론이 나온다.

\[\displaystyle S=\sum_{d|n} {(d-1)\times{(2^{(n/d)-1}-1)}}\]

하지만 여기에는 맹점이 있다. 예를들어 전체를 12개의 구간으로 쪼개는 경우의 수가 존재한다고 하면, 이는 이미 1, 2, 3, 4, 6 개의 구간으로 쪼갠 경우의 수에서 중복으로 여러번 세지기 때문이다. 따라서 이를 보정할 필요가 있다. 아래와 같은 그림을 생각해 보자.

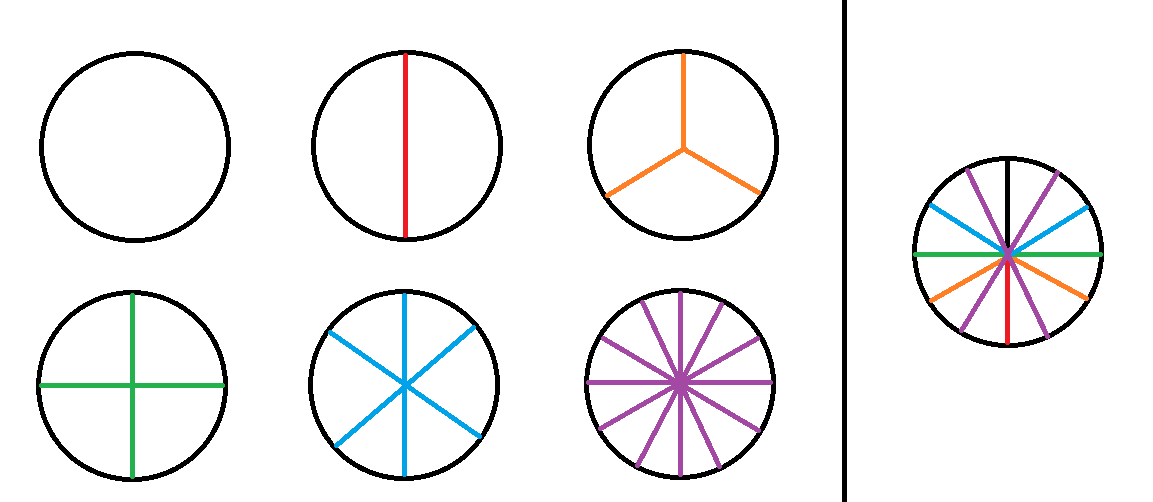
왼쪽 6개의 원을 보면 서로 겹치는 선이 존재함을 알 수 있고, 12개로 구간이 쪼개진 경우는 각각에 대하여 겹치는 횟수만큼 더 많이 세어졌음을 알 수 있다. 따라서 선을 한곳에 몰아서 그은 뒤(오른쪽 그림을 보자), 매번 새롭게 추가되는 선의 개수만큼만 추가를 해주어야 하며, 이는 분수로 나타내었을 때 서로소인 쌍의 개수이므로 $\phi(d)$ 로 앞서 구한 식의 $(d-1)$ 부분을 고쳐야 된다. 따라서 구하고자 하는 경우의 수는 아래와 같다.

\[\displaystyle S=\sum_{d|n} {\phi(d)\times{(2^{(n/d)-1}-1)}}\]

1~n 까지의 오일러 피 함수 값은 에라토스테네스의 체와 유사하게 전처리를 통해 $O(n\log{\log{n}})$ 에 가능하고, 약수를 구하는데 $O(\sqrt{n})$, 2의 거듭제곱 역시 전처리로 $O(n)$ 에 해결이 가능하다. 또한 위의 식 계산은 ($n$의 약수의 개수$\leq 2^{\log{n}/\log{\log{n} } }$) 이므로 굉장히 작은 시간이 걸림을 알 수 있다. 따라서 전체 시간 복잡도는 $O(n\log{\log{n}})$ 이 된다. 실제 정답은 위의 계산된 값에 $(n-2)$ 를 곱한 $S\times{(n-2)}\pmod{p}$ 가 된다. 참고용으로 코드를 덧붙인다.

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back

using namespace std;
typedef long long ll;
typedef pair<ll,ll> P;

int n, phi[1000005];
ll mod, pw[1000005];
vector<int> d;

int main()
{
    scanf("%d %lld",&n,&mod);
    pw[0]=1;
    for(int i=1 ; i<=n ; i++) phi[i]=i, pw[i]=(pw[i-1]*2LL)%mod;
    for(int i=2 ; i<=n ; i++){
        if(phi[i]==i){
            for(int j=i ; j<=n ; j+=i) phi[j]-=phi[j]/i;
        }
    }
    ll ans=0;
    for(int i=2 ; i*i<=n ; i++){
        if(n%i==0){
            d.pb(i);
            if(i*i!=n) d.pb(n/i);
        }
    }
    for(int v : d){
        ll tmp=pw[(n/v)-1]-1;
        if(tmp<0) tmp+=mod;
        (ans+=phi[v]*tmp)%=mod;
    }
    (ans*=n-2LL)%=mod;
    printf("%lld",ans);
    return 0;
}