개요
이 포스팅에서는 최근 앳코더에서 자주 출제되고 있는 Re-rooting DP에 대하여 소개하도록 한다.
트리 DP
Re-rooting DP를 시작하기 위해서는 기본적으로 트리 DP를 알고 있어야 한다. 트리 DP는 말 그대로 트리에 주어진 문제를 해결하는 방법을 DP로 하면 된다. 예를 들면 트리에서의 최대 매칭을 찾는다던가, 최대독립집합을 찾는데 이용될 수 있을 것이다.
간단하게 트리에서의 최대독립집합을 구하는 문제인 BOJ 2533 사회망 서비스(SNS)를 풀어보도록 하자. 일반적으로 unrooted tree가 주어지면 1번 정점을 루트로 하는 rooted tree로 바꾸어 문제를 해결하게 된다. 또한 당연히 DP를 이용하므로 점화식을 세워야 할 것이다. 점화식은 아래와 같다.
$D(i,0)=i$번 정점을 루트로 하는 서브트리에서 정점$i$가 얼리어답터가 아닌 경우, 최소 얼리어답터의 수
$D(i,1)=i$번 정점을 루트로 하는 서브트리에서 정점$i$가 얼리어답터인 경우, 최소 얼리어답터의 수
$\displaystyle D(i,0)=\sum_{j\in{\mathrm{childs\ of}\ i}} {D(j,1)}$
$\displaystyle D(i,1)=1+\sum_{j\in{\mathrm{childs\ of}\ i}} {\min (D(j,0),D(j,1))}$
자명하게 정답은 $\min(D(1,0),D(1,1))$ 이 될 것이다.
Re-rooting DP?
그렇다면 Re-rooting DP란 무엇일까? 위에서 언급한 바와 같이 일반적으로 트리 DP를 할 때 우리는 1번 정점을 루트로 잡고 문제를 해결한다. 또한 대부분의 문제는 전체 트리에서의 정답만을 요구하므로 1번 정점에 정답이 기록되는 구조를 갖는다. 하지만 몇몇 문제의 경우 루트가 어디인지에 따라 답이 달라지기도 하는데, 이런 경우를 효율적으로 처리하는 방법이 Re-rooting DP이다. 예시 문제를 하나 가지고 와서 해결해보자.
위의 문제를 푸는데 필요한 점화식은 앞서 언급한 SNS 문제와 유사하게 세우면 되므로 생략하도록 하겠다. 본 문제는 전체 트리에서의 최대 매칭을 찾은 뒤, 그 값과 정점 1개를 제거한 상태에서의 최대 매칭이 서로 같은 경우의 개수를 구해야 한다. 쉽게 추측 가능하겠지만 정점 $i$가 제거되었을 때의 최대 매칭을 찾는 문제는, 정점 $i$를 루트로 하는 rooted tree에서 정점 $i$가 매칭이 되지 않는 경우에 대한 최대 매칭을 구하는 것과 동치이다.
그렇다면 일단 전체 트리에서의 최대 매칭을 구한 뒤, 각 정점을 루트로 잡고 최대 매칭을 계산하면 문제는 풀릴 것이다. 단순히 모든 정점을 루트로 잡고 문제를 해결하면 $O(n^2)$ 의 시간이 걸릴 것이고, 이는 주어진 문제를 해결하는데 부적절한 시간 복잡도이다. 하지만 Re-rooting DP를 이용하면 $O(n)$ 에 우리가 구하고자 하는 값을 구할 수 있게 된다.
 |
 |
|---|---|
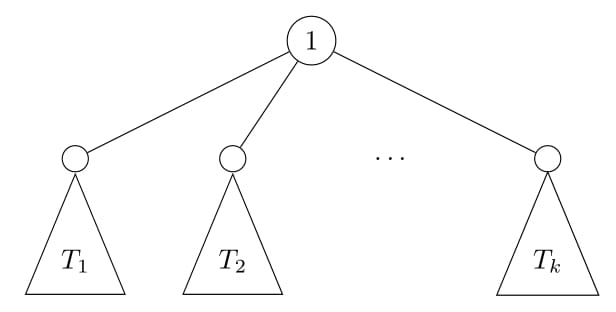
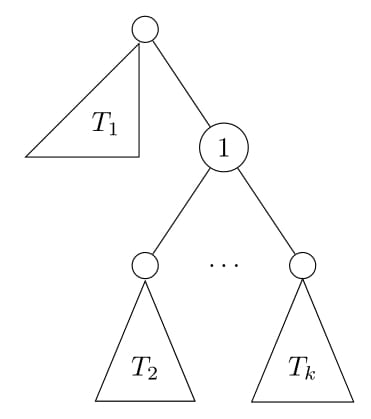
| Figure 1 | Figure 2 |
Re-rooting DP의 핵심 아이디어는 다음과 같다. 일단 1번 정점을 루트로 하는 일반적인 트리 DP를 통해 값을 구해놓은 상태라고 하자. 그렇다면 Figure 1과 같은 상황에서 각 서브트리 $T_1,T_2,\ldots,T_k$에 대한 정답은 이미 구해져 있을 것이다. 이때 트리의 루트를 서브트리 $T_1$ 의 루트로 바꾼다고 하자. 그러면 트리는 Figure 2와 같이 변하게 된다. Figure 1에서 Figure 2로 바뀌었을 때 이전의 트리에서 새롭게 계산해야 할 부분이 얼마나 되는지 생각해보면, 1번 정점을 루트로 하는 서브트리와 새로운 루트의 서브트리(=전체 트리) 이렇게 2부분만 업데이트하면 됨을 알 수 있다. 즉, 모든 계산을 다시 할 필요가 없다는 뜻이다.
그렇다면 우리는 이제 1번 정점에서 자신의 자식 노드들로의 re-rooting은 쉽게 가능하단 것을 알고있다. 하지만 re-rooting은 1번 정점의 자식 노드들에게만 일어나지 않는다. 따라서 다른 노드들은 어떻게 해야할지 생각해보아야 할 것이다. 이 문제는 상당히 간단하게 해결이 된다. re-rooting이 끝났다는 것은 이제 Figure 2의 상태를 다시 Figure 1과 같은 상태로 바라볼 수 있다는 뜻이다. 따라서 나머지 노드들에 대하여도 같은 방식을 적용하여 쉽게 re-rooting이 가능함을 알 수 있고, 이는 dfs를 이용하여 구현하면 편할 것이라는 추측이 가능하다.
구현
이제 실질적으로 구현이 어떤식으로 이루어지는지 알아보도록 하자. re-rooting을 하기 위해서는 기본적으로 1번 정점을 루트로 하는 트리에 대하여 문제를 해결하고, 그 이후 dfs를 돌면서 값들을 수정하게 된다. 값을 수정하기 위해서는 참조해야할 값들이 이미 DP를 통해 구해진 값들도 있지만, dfs를 돌면서 매번 수정되는 값 또한 존재한다. 수정되는 값은 이전에 루트였다가 이제는 자식이 된 노드의 값이고, 이 값은 dfs에 인자로 같이 넘겨주면 깔끔하게 구현이 가능하다. 대략적인 Re-rooting DP 의 형태를 정리하면 아래와 같다.
1번 정점을 루트로 하여 DP를 수행
이후 dfs를 돌며 re-rooting을 진행한다
// cur = 현재 정점(즉, 새로운 루트), prev = 이전 정점(즉, 과거의 루트)
// val = 새로운 계산을 위한 과거의 루트에서의 DP 값
rerooting(cur, prev, val)
- val 값 등을 참조하여 cur에 대한 DP 값 재 계산
- cur의 인접 정점(=nxt)으로 이동하여 rerooting(nxt,cur,new_val)
// new_val = nxt로 이동하는데 필요한 DP 값
이해를 돕기위해 예시로 들었던 문제의 코드를 첨부하겠다. 코드
Re-rooting DP를 이해를 제대로 했다면, 위에서 설명한 내용이 단순히 DP에만 적용가능한 경우가 아님을 눈치챌 수 있을 것이다. 사실상 Re-rooting의 본질은 이미 계산을 마친 상태에서, 새로운 루트로 바꿀 때 수정될 내용이 별로 없다는 점이다. 따라서 DP 뿐만이 아닌 더욱 다양한 문제에 출제가 될 수 있으며, 세그먼트 트리와 연관되는 경우 오일러 경로 테크닉과 함께 사용될 수도 있다. 이와 관련된 연습 문제를 하나 첨부하고 글을 마치도록 하겠다.